1. 들어가기 전에
이번 글은 이전 글들과 조금 다른 성격으로, 특정 지식의 전달보다는 프로젝트 풀이를 위해 했던 생각들을 위주로 전달할 예정이다. 따라서 문제 해결을 위한 모든 방법이 아닌 특정 방법만 소개될 예정이며, 글 전체적으로 주관적인 성격이 강하므로 이를 참고하고 읽는 것을 추천한다. 풀이를 위해 어떤 흐름으로 생각을 했는지 정도를 보면 좋을 것 같다.
또한 대충 어느 정도의 값이 나올지 예측은 되는데, 수식으로 정리하려고 보니 잘 안 되었다. 시간 복잡도 계산에 있어서 얼마나 무능한지 알 수 있었다. 알고리즘 문제를 푼다든가, 어떤 것에 대해서 코딩을 할 때 지금보다도 더 꼼꼼하게 시간 복잡도를 확인하고 증명하는 습관을 들여야겠다는 생각을 많이하게 되었다.
이번 과제의 경우에도 결과적으로는 과 같은 형태로 코드를 작성했는데, 순수하게 으로 돌지 않는다는 확신 하나만으로 결과를 내보았다. 프로젝트에서 좋은 점수를 받을 만큼의 결과가 나왔고 이는 얼추 예측한 범위 내에서 나왔음에도, 제시된 알고리즘이 의 정렬과 비슷하거나 조금 더 좋은 결과를 내는 것에 대해서 정확한 수식으로 증명하지 못했다. 반성해야할 부분이라고 생각하고, 상당히 부끄럽게 느껴진다.
다시 공부해야 할 것 같다 ㅎㅎ..
2. Approach
1) 중복 검사
push_swap에서는 숫자로 되어 있는 인자만 받을 수 있으며, 인자 값은 중복으로 받을 수 없다. 따라서 중복된 값으로 인자가 들어왔을 때, 이를 확인하고 적절하게 에러를 내줘야 한다.
정렬을 수행하는 로직을 어떻게 두지 정하지 않은 상태이더라도, 평가 기준에 부합하는 결과를 내기 위해선 평균적으로 의 성능이 보장되어야 한다. 정렬에서의 평균 시간 복잡도를 을 만족하더라도 중복 검사를 수행할 때 인자들을 일일이 확인하게 된다면 이 되어버린다. 운이 좋다면 까지 걸리지 않겠지만, 이는 어디까지나 중복된 인자가 들어간 경우에만 해당된다. 즉, 중복된 인자가 들어오지 않고 정상적으로 정렬 로직을 수행하게 된다면 이미 확정적으로 을 수행하는 것이 되므로 중복 검사에 조금 더 효율적인 방식이 필요하다.
중복 검사를 위한 방법은 크게 3가지가 떠올랐다.
1.
각 인자 별로 다른 인자들을 일일이 비교하는 방법 Brute Force
2.
사용된 인자들을 테이블에 기록하는 방법 Memoization
3.
집합 Set
가장 쉬운 방법은 1번이지만, 위에서 언급한 것처럼 시간 복잡도를 만족하기 위해서 사용할 수 있는 방법은 아니었다. 이 커질수록 중복 검사를 위해 소요되는 시간이 커지기 때문이다.
가장 시간이 적게 걸리는 방법은 2번이었지만, 이 역시도 사용할 수는 없는 방법이었다. Memoization 방식은 사용하려는 인자들의 만큼의 공간을 할당해두어, 라는 값이 사용되었으면 할당 받은 공간의 번째 index에 해당하는 곳에 마킹을 해두는 방식이다. 일반적인 로직 테스트를 위해 인자들의 Interval이 1인 형태로 입력이 들어오는 경우에는 문제 없이 사용할 수 있지만, Interval이 무작위 하게 인자들이 들어오는 경우에는 중복 검사를 위한 공간이 굉장히 Sparse할 수 있다는 것이 가장 큰 문제이다. 예를 들어 1 2 3 4 5와 같은 형태로 인자를 받게 되면 할당 받은 5개의 공간을 문제 없이 이용할 수 있지만, -2147483648 1 2 3 4 5와 같은 형태로 인자를 받으면 할당 받은 공간을 Sparse하게 이용하게 되는 것이다. 해당 경우에 사용하는 인자는 6개지만, -2147483647 ~ 0까지의 공간은 낭비하게 된다.
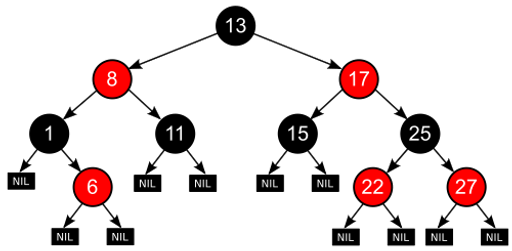
따라서 공간을 낭비 없이 효율적으로 사용하면서 보다 적은 시간 내에 원하는 결과를 얻기 위해 떠올린 것이 Set이었다. Red-Black Tree로 구현된 Set은 1개의 요소를 삽입할 때 걸리는 시간이 이며 탐색이 포함되어 있기 때문에, 삽입 연산만으로 중복 검사를 수행할 수 있다. 즉, 개의 요소를 삽입할 때는 이 요구되며 이 과정에서 중복 인자가 들어왔는지 판별이 가능해진다.
Red-Black Tree?
Red-Black Tree는 이진 탐색 트리의 한 종류이다. 이진 탐색 트리의 특성 상 Balance를 잘 유지하지 못하면 에 근접한 성능이 나오게 되는데, Red-Black Tree는 삽입 연산 후 Balance가 유지될 수 있도록 자체적으로 균형을 조정하여 삽입, 삭제, 탐색의 Worst Case에 대해서도 항상 의 성능을 보장한다. 균형을 조정할 때는 상황에 따라 Left Rotation 혹은 Right Rotation을 수행하여 내부에 유지 중인 Node들을 회전시킨다. 상대적으로 AVL Tree 보다는 균형에 대한 기준이 엄격한 편은 아니어서 Worst Case에 AVL Tree보다 적은 Rotation을 수행하므로 고정된 의 성능을 보장할 수 있는 것이다.
2) Stack
처음에 후보로 두었던 Stack의 자료구조는 배열, 덱, 리스트로 총 3개였다.
이용하려는 인자의 수만큼을 공간을 할당 받아 배열을 이용한다고 했을 때 생각났던 문제점은 2개였다. push 연산을 반복했을 때 남는 공간이 많아지는 문제와 rotation 연산을 반복했을 때 인자를 적절히 위치시키기 위해서 모든 인자들을 앞 혹은 뒤로 한 칸씩 밀어줘야 한다는 문제가 있는데 이를 해결할 수 있어야 했다. 첫 번째 문제는 그냥 신경 쓰지 않고 구현하더라도 두 번째 문제만큼은 차라리 리스트를 이용하는 것이 더 낫겠다는 생각이 들었기 때문에 배열은 후보지에서 제외시켰다.
덱의 경우에는 간단하게 배열을 보유하고 있는 리스트들의 연결로 구현할 계획으로 실제 덱의 블록 구조와 최대한 비슷하게 생각을 했었다. 이렇게 구현을 하게 되면 위에서 제시한 rotation 연산으로 인자의 앞 뒤로 붙이고 미는 과정이 필요 없고 그저 이전 인덱스에 해당하는 공간에 값을 기록하기만 하면 되므로 문제가 되지 않는다. 하지만 여전히 push 연산으로 인한 남은 공간에 대한 낭비가 있다는 점은 해결되지 않을 것 같았다. 더군다나 덱은 블록이라는 구조 때문에 일반적인 자료구조보다 더 큰 메모리를 차지하며 시간 상의 득을 보는 구조이므로 단순히 정해진 크기의 공간만 낭비 되는 것이 아니라 사용하고 있는 공간 외의 나머지 공간에 대해 소모가 있을 수 있어서 후보지에서 제외시켰다.
결과적으로 일반적인 Stack을 구현하는 것처럼 리스트를 이용하기로 했다. rotation 연산을 고려해서 순회 구조로 구현할 계획이었고, 각 Node를 Single로 연결할지 Double로 연결할지만 정하면 되었다. 결과적으로는 Double로 구현을 했는데, 생각해보면 Single로도 충분했을 것 같다.
구현 초기에는 Single로 두고 진행했지만, 코드를 작성하는 과정에서 로직을 많이 뒤엎다보니 Double로 바꾸었다가 Single로 바꾸었다가 하는 과정을 반복하게 되었다. 어떤 로직으로 결과를 낼지 모르는 상황이어서 Double로 진행을 했다가 이 형태 그대로 놔두게 되었다. 프로젝트를 마친 후에 보니 Single로 해도 무방한 로직이었던 것 같은데 Double로 한 것이 많이 아쉬웠다.
3) Sorting
1. Divide and Conquer (ver. 1)
기본적으로 평가 기준에서 제한하는 명령어의 제한을 맞추기 위해선 의 방법으로는 맞출 수 없기 때문에 의 방법을 찾아보아야 한다. 은 개의 인자들에 대한 결과이므로 간단하게 생각해서 1개의 인자는 정도로 처리 되어야 함을 알 수 있다.
따라서 가장 먼저 떠올린 방식은 Divide and Conquer (분할 정복)이었다. 절반을 나누어 B Stack으로 밀고 남은 절반을 A Stack에서 정렬하고, A Stack 정렬을 위해 다시 절반을 나누어 B Stack으로 밀고 남은 절반을 A Stack에서 정렬하고... 특정 개수가 되어 정렬을 할 수 있을 때까지 재귀적으로 정렬 함수를 호출하는 식으로 구상을 했다.
위와 같은 방식으로 작성을 했을 때, 상당히 만족스럽지 못한 결과가 나왔다. 100개짜리 인자와 500개짜리 인자에서 아예 점수를 못 받을 만큼이었던 것으로 기억한다. 최적화를 하면 조금 더 나을 수 있겠지만, 최적화 전부터 너무 큰 차이를 보여 다른 방법을 떠올렸다.
2. Divide and Conquer (ver. 2)
다음으로 생각한 것이 정확히 절반으로 나누어 함수를 호출하는 것보다는 가장 많이 정렬이 되어 있는 값을 기준으로 삼아 반을 나누는 식으로 재귀적으로 함수를 호출하게 되면 조금 더 나을 것이라고 생각했고, 이전에 작성했던 로직에서 B Stack으로 넘기는 값들을 이 방법으로 수정했다. 전반적으로 명령어 반복 횟수가 줄었지만, 이 역시도 만족스러운 결과를 내지 못했다. 정해진 규칙에 맞춰서 나누는 것이 어쨌든 좋은 방향으로 가는 것 같아서 조금 더 좋은 방법을 고민해보았다.
3. Divide and Conquer (ver. 3)
이전과 마찬가지로 가장 많이 정렬되어 있는 값을 기준으로 삼는 것은 동일하지만 반을 나누는 것이 아니라 3분할을 생각해냈다. 이전 방법은 정렬되어 있는 값을 기준으로 큰 값 혹은 작은 값을 이용하여 진행했었는데, 두 값 어느 것을 이용해도 반을 나누는데는 명령어 횟수가 비슷한 것을 볼 수 있었다. 이번에는 이 두 값을 동시에 이용해보는 것은 어떨까하는 생각이 들었다. 이 방법은 minckim님께서 작성하신 방법과 그 방법이 대체적으로 굉장히 비슷하다.
3분할을 해놓은 chunk들이 정렬되기 위해선 가장 큰 chunk를 A Stack에 두고, 이를 정렬하기 위해 재귀를 호출하는 방식이 된다. 그리고 재귀를 반복하게 되면 중간 chunk를 B Stack의 뒤에 두고, 가장 작은 chunk를 B Stack의 앞에 두도록하여 쌓이게 된다. 이후에 A Stack에 정렬을 마치게 되면 Call-Tree에서 호출을 회수하면서 B Stack에 쌓인 chunk들을 A Stack으로 옮겨주어야 하고, 마찬가지로 정렬이 된 chunk를 A Stack으로 옮기거나 A Stack으로 옮긴 뒤에 해당 chunk를 정렬하는 과정이 필요하다. 이렇게 옮겨진 chunk가 정렬이 되었다고 해서 A Stack 전체가 정렬이 된 형태는 아닐 수 있으므로, A Stack 전체를 다시 정렬하기 위해 재귀를 호출하는 구조를 가져야 한다.
이전 분할 정복과 마찬가지로 명령어 횟수에 큰 차이는 없었다. 전체적으로 정렬이 되어 있는지 확인하면서 추가적으로 재귀를 호출하는 횟수가 많았고, 이에 따라 불필요하게 호출되는 push와 swap들이 많았다. 추가적인 최적화를 하면 명령어가 많이 줄어들까 싶은 생각이 들었는데, 결국에는 포기하고 다른 방법을 찾아나섰다.
이 방법으로 명령어들을 정해진 횟수에 만족시키도록 코드를 작성한 분들께서는 최적화를 굉장히 잘한 것이라고 생각이 드는데, 어떻게 최적화 했는지 개인적으로 무척 궁금하다.
이와 같은 증상이 발생했던 이유를 알게 되었다. Pivotting에 문제가 있었던 것이다. , 지점에 바로 Pivotting을 하는 것보다, 정렬하려는 구간의 정렬된 값에 대해서 , 지점을 Pivotting을 하면 불필요한 push와 swap들을 정말 많이 없앨 수 있었다. Pivotting의 중요성을 다시 한 번 깨달을 수 있었다. 초반에는 왜 정렬된 상태의 지점 값을 이용할 생각을 안했는지 모르겠다 ㅎㅎ...
4. Predicate
리프레쉬를 할 겸 여러 알고리즘들을 찾아보다가 결국에 Quick Sort의 특성을 다시 한 번 생각해보게 되었다.
Quick Sort는 다른 정렬 알고리즘과 달리 고정적으로 이라는 성능을 보장하지 않고, 평균적으로 의 성능을 낸다. 즉, Worst Case에는 이 되는 알고리즘이라는 것이다. 그럼에도 Quick Sort가 충분히 빠른 정렬인 이유는 다른 정렬 알고리즘들처럼 고정된 방식으로 정렬을 수행하는 것이 아니라, 정렬을 수행하려는 값들에 의존하기 때문이다. 정렬을 수행하려는 값들이 얼만큼 정렬이 되어 있는지가 큰 영향을 끼치게 된다.
또 다른 특성으로는 Quick Sort 자체가 Stack을 이용하여 정렬을 수행하게 되고 이 때 사용되는 연산들이 이번 프로젝트에서 사용되는 연산들과 대체적으로 유사하다는 것이었다. Quick Sort에서 사용하는 Stack이 일반적인 Stack이 아니라 사용자가 정의한 Stack을 이용하여 구현한 경우에는 조금 더 나은 성능을 보일 수 있다는 얘기가 떠올라, 이번 과제가 정말 큰 틀 안에서 Quick Sort와 다를 것이 없구나 싶었다. push_swap에서는 특정 명령어를 수행할 수 있는 사용자 정의 Stack이 있으므로, 이를 이용 했을 때 연산이 높게 나올만한 원인을 찾아보게 되었다. 이전까지의 구현 방법들을 보면, push와 swap을 이용했을 때 대체적으로 각 Stack이 Mess-Up되어 다시 재귀를 호출하고 그 호출 횟수가 많아지는 느낌을 많이 받았었다.
얼만큼 정렬이 되어 있는가와 명령어 횟수를 높게 만드는 명령어를 고려해서 로직을 떠올려보기로 했다. 그렇게 떠오른 방식이 수행하게 될 명령어가 가장 적은 값을 이용하는 방식이었다.
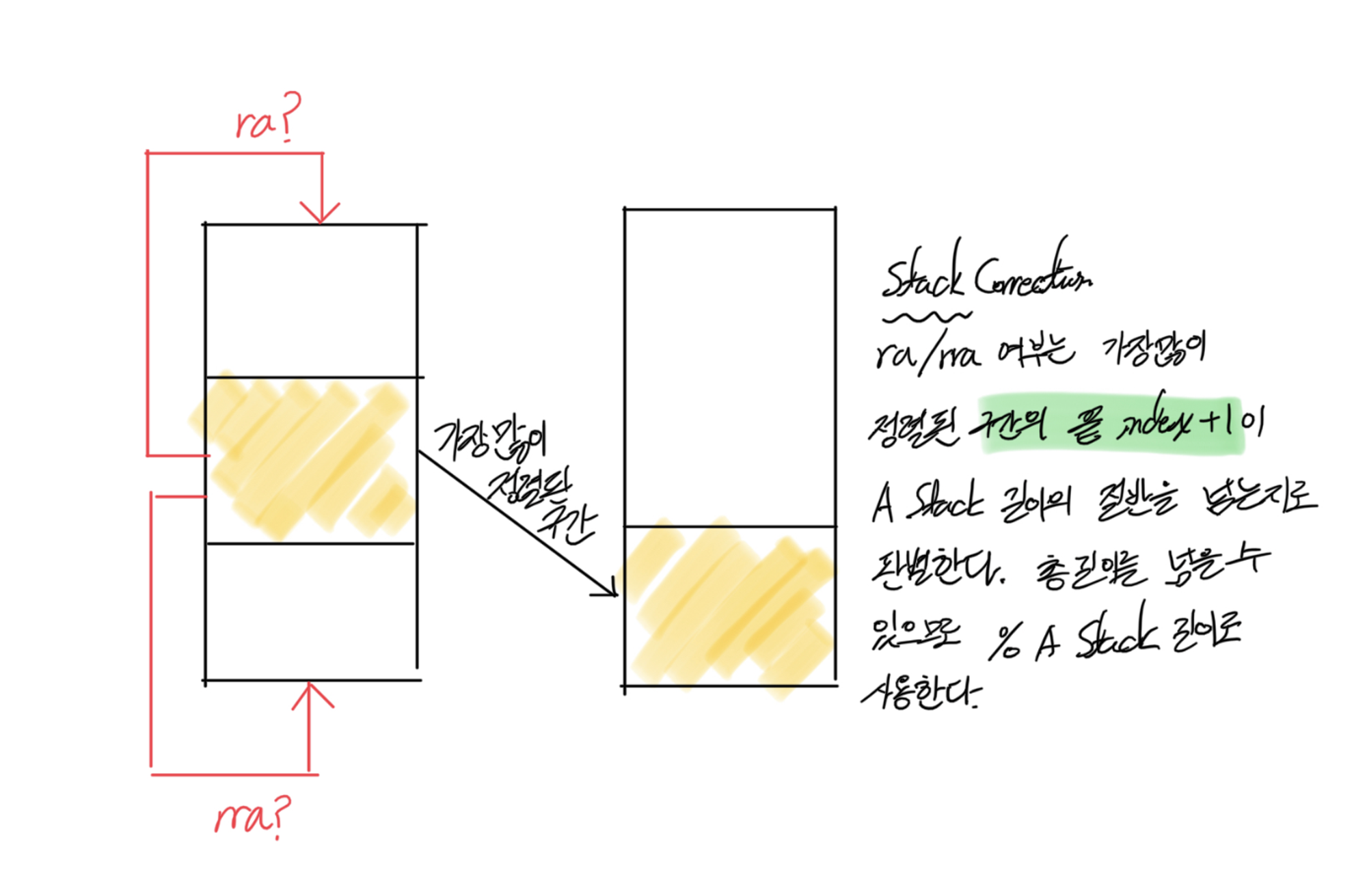
가장 많이 정렬이 되어 있는 구간을 찾아내고, 그 구간을 A Stack의 바닥에 위치할 수 있도록 rotation을 수행한다. 이 때 CW (clock-wise)로 돌릴지, CCW (counter clock-wise)로 돌릴지는 적절히 판단하여 수행할 수 있도록 만든다. 이와 같이 정해진 위치의 값을 A Stack의 가장 아래에 깔아두는 과정을 Correction이라 하겠다. Correction을 거치게 되면 위 그림처럼 가장 많이 정렬되어 있는 구간은 아래로 깔리고 나머지 값들은 A Stack의 위에 위치하게 되는데, 그 다음에는 구간 외의 값들을 모두 B Stack으로 넘기는 A to B를 수행한다.
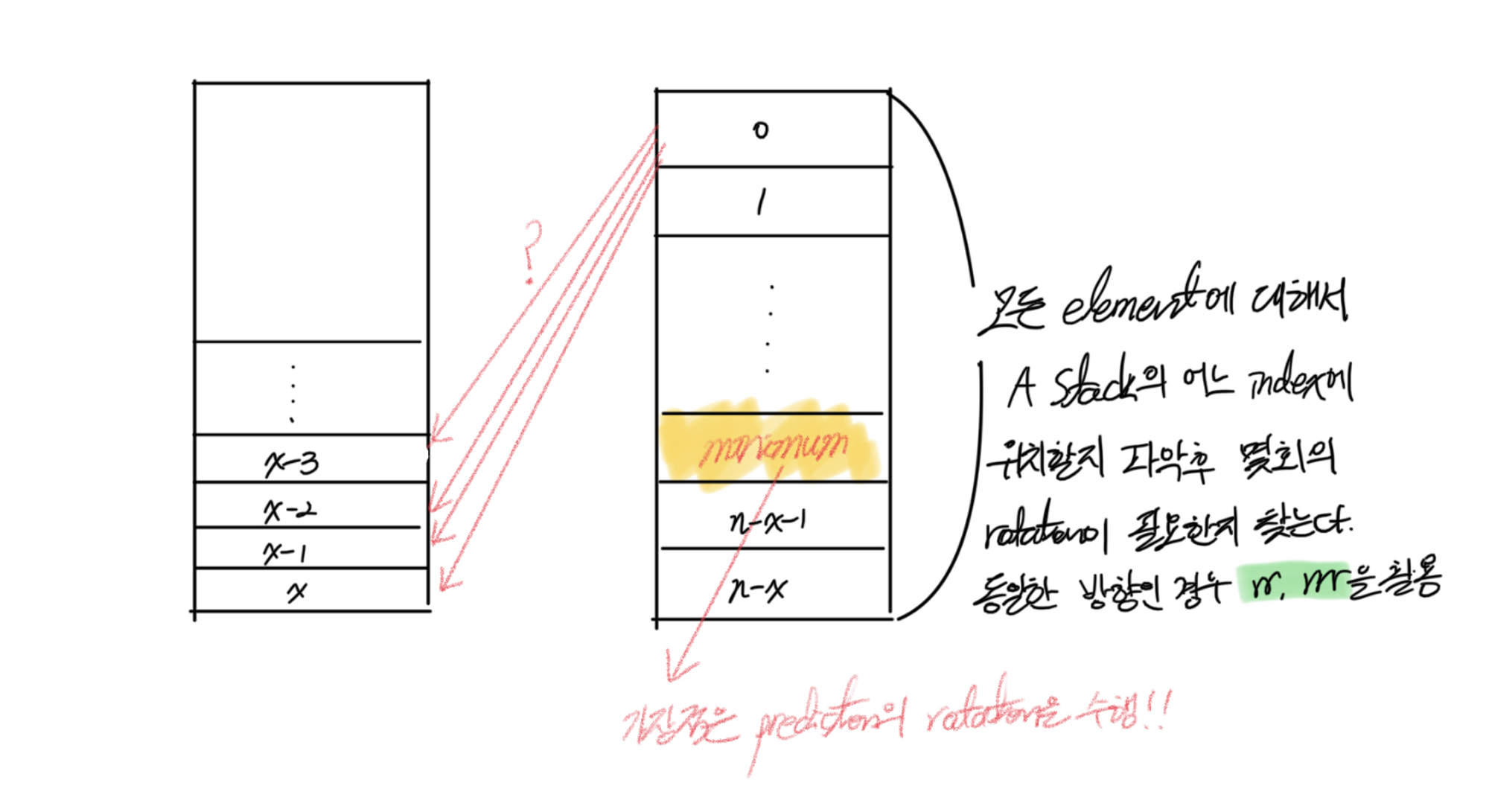
이제는 A to B로 넘어온 인자들을 하나 하나 A Stack으로 넘겨주는 과정이 필요한데, 이를 B to A라고 해보자. 이 때 B Stack에 위치한 값들이 A Stack의 제 위치로 찾아가기 위한 명령어 횟수를 미리 계산해보고 가장 적게 소요되는 인자를 A Stack에 옮기도록 만든다. 이를 B Stack에 있는 값들이 없어질 때까지 반복하면 된다. 여기서 B Stack의 각 인자들이 사용할 명령어 횟수 등의 정보를 계산한 것을 Predicate이라 한다.
이와 같이 하면 A Stack에 정렬되어 있는 값들이 개라고 했을 때 pa와 pb를 호출하는 횟수는 가 되고, 값을 확정적으로 옮길 때 외에는 push는 사용되지 않는다. 또한 적은 인자를 정렬하는 것이 아니라면 이와 같은 일반적인 인자들을 정렬할 때는 별도의 swap이 사용되지 않는다. 따라서 순수하게 rotation만으로 정렬을 수행하게 되고, 이는 rotation 수행 전에 명령어를 파악할 때 cw 혹은 ccw 중 더 작은 값으로 명령어를 수행할 수 있게 된다. 따라서 rotation에 대해서는 별도의 메모리를 할당받고 후처리를 하는 식으로 최적화를 하지 않아도 된다.
탐색 방식은 1회차에는 번, 2회차에는 번, ... , 회차에는 1번이 되어 Big-O Notation으로는 이 되지만, 실제로는 순수한 보다는 적은 연산이 돌아가면서 A Stack 내의 인자들이 많이 정렬이 되어 있을수록 더 적은 시간이 소요된다. 명령어 수행 측정에는 탐색 과정이 포함되지 않기 때문에 명령어 수행 횟수를 따로 생각하여 처럼 동작하는지 생각해봐야 하는데 이 역시도 에 미치지 않는다는 것을 떠올릴 수 있다. 의사 코드는 아래와 같다.
// pseudo-code
func do_before_sort()
{
// 가장 길게 정렬되어 있는 구간을 찾는다.
find_longest_sort()
// 찾은 위치를 토대로 해당 구간이 A Stack 가장 아래에 위치할 수 있도록 rotation을 수행한다.
// rotation은 구간의 끝 index + 1이 A Stack 절반보다 큰 지 작은 지 판별하여 cw, ccw를 수행한다.
stack_correction()
// Stack Correction 이후에 가장 길게 정렬되어 있는 구간의 index가 바뀌어 있을 수도 있다.
// 따라서 구간 검색을 다시 한 번 해주어 a_to_b 호출 시 이미 정렬되어 있는 값이 B Stack으로 가지 않도록 한다.
find_longest_sort()
}
func a_to_b()
{
while A Stack의 모든 lst에 대해서
if current lst index < 정렬되어 있는 구간의 시작 index
do pb
}
func b_to_a()
{
do 임시 predicate 초기화
while B Stack의 lst가 존재하지 않을 때까지
{
do 최소 predicate 초기화
while B Stack의 모든 lst에 대해서
{
do current lst에 대해 소요되는 명령어 횟수를 임시 predicate에 기록
if 최소 predicate > 임시 predicate
최소 predicate := 임시 predicate
}
do predicate에 기록된 횟수만큼 A Stack과 B Stack을 rotation
do pa
}
}
func sort_3()
{
// do_before_sort에서 이미 최소 2개는 정렬이 되어 있다.
// 따라서 do_before_sort 과정 이후에도 정렬이 안 되어 있는 경우는 총 2가지다.
// 2 1 3 -> sa 수행
if current lst val > next lst val && current lst val < next next lst val
do sa
// 3 1 2 -> ra 수행
else if current lst val > next next val
do ra
}
func sort_5()
{
// A Stack의 길이가 4인 경우에는 do_before_sort에서 찾은 구간의 크기가 2, 3이 된다.
// A Stack의 길이가 5인 경우에는 do_before sort에서 찾은 구간의 크기가 2, 3, 4가 된다.
// 3개짜리 정렬 로직이 있으므로 현재 함수에서 최대한 3개짜리 정렬 로직을 활용한다.
// 구간의 크기가 2인 경우에는 A Stack에 인자를 3개가 되도록 만들고 이를 정렬한다.
if 정렬된 구간의 크기 < 3
{
do A Stack에 3개만 남기고 B Stack으로 push
sort_3()
}
// 구간의 크기가 3이상인 경우에는 구간에 해당하지 않는 값을 B Stack으로 넘기는 함수를 호출한다.
else
a_to_b()
// 이 후에는 A Stack에는 최소 3개 이상이 정렬되어 있는 상태고 나머지는 B Stack에 위치한다.
// 따라서 b_to_a를 호출하여 B Stack의 인자들이 A Stack에 제 위치에 있도록 만들어준다.
b_to_a()
// B Stack의 인자들을 A Stack으로 옮긴 후에는 최소 인자가 가장 앞에 와있지 않을 수 있다.
// 따라서 A Stack에서 가장 작은 값을 찾아 Stack Correction을 수행한다.
stack_correction()
}
func sort_others()
{
a_to_b()
b_to_a()
stack_correction()
}
func yield()
{
// do_before_sort에서 가장 길게 정렬된 구간을 찾는다.
// 찾은 구간으로 Stack Correction을 거치므로 최소 2개의 인자는 정렬이 되어 있게 된다.
do_before_sort()
if A Stack의 길이 < 2
return
else if A Stack의 길이 == 3
sort_3()
else if A Stack의 길이 <= 5
sort_5()
else
sort_others()
}
C
복사
5. 특정 개수 이하의 정렬
2개짜리는 가장 길게 정렬되어 있는 구간을 찾고 Correction을 하는 과정에서 이미 정렬이 되어버리고, 3개짜리는 Correction 후 sa 혹은 ra만으로 끝나게 된다.
4개짜리와 5개짜리는 Correction 후에 A Stack에 3개만 남기고 나머지를 B Stack으로 옮긴다. 그리고 A Stack을 3개짜리 정렬 방식으로 정렬 후, B Stack에 있는 값을 Predicate 방식을 이용하여 정렬한다.
3. Testing Script
checker 부분과 push_swap 부분으로 나누어 작성하였고, Makefile에 test라는 Rule을 추가하여 테스트를 수행하였다. test라는 Rule에는 checker_test와 push_swap_test라는 Rule이 의존성으로 존재하고, 각 Rule이 checker와 push_swap에 해당하는 스크립트를 실행하도록 작성했다.
스크립트 내부에는 테스트에 사용될 인자들을 수기로 작성한 것들도 있었고, 작성한 Sorting Algorithm에 대해서 평균적인 성능을 측정해보기 위해 무작위 난수를 생성 후 특정 횟수만큼 반복하여 결과를 측정하는 식으로 작성해두었다. 작성 초기에는 C++을 이용하여 별도의 실행 파일을 만들어서 난수를 얻었는데, 평가 환경 및 작업 환경이 Mac OS X므로 기본적으로 설치되어 있는 ruby를 그대로 이용해도 좋겠다는 생각이 많이 들었다. 결과적으로는 ruby의 옵션을 통해서 난수를 생성하도록 두었다.
그 외에는 Makefile에는 표준 에러로 나오는 출력에 대해서는 false로 인식하여 오류로 처리하므로, 표준 에러의 출력을 검증할 때 false가 나오지 않도록 신경 써주었다.
아래 항목에 기재된 링크에는 소스 코드들이 있다. 소스 코드에서 test라는 디렉토리에 있는 스크립트들을 실행하는 방식 그대로 활용해도 좋고, Makefile에 Rule을 두는 식으로 활용해도 좋으므로 필요하다면 가져다 사용해도 좋다.